20250929 Senior Varsity Training

Problem 1

Equilateral $△ABC$ with side length $14$ is rotated about its center by angle $\theta$, where $0<\theta <60°$, to form $△DEF$. See figure. The area of hexagon $ADBECF$ is $91\sqrt{3}$. What is $\tan (\theta )$?

Solution

Let $O$ be the center of $△ABC$, then it is easy to prove that

$$\begin{array}{rl}|OA|& =\frac{\sqrt{3}}{3}|AB|\\ & =\frac{14\sqrt{3}}{3}\end{array}$$

It is easy to prove that

$$\begin{array}{rl}[ADBECF]& =3[△OAD]+3[△OAF]\\ & =\frac{3}{2}|OA{|}^2\sin (\theta )+\frac{3}{2}|OA{|}^2\sin (120°-\theta )\\ & =98\sin (\theta )+98\sin (120°-\theta )\end{array}$$

Therefore,

$$\begin{array}{rl}[ADBECF]=91\sqrt{3}& ⟺\sin (\theta )+\sin (120°-\theta )=\frac{91\sqrt{3}}{98}\\ & ⟺\frac{1}{2}\cos (\theta )+\frac{\sqrt{3}}{2}\sin (\theta )=\frac{91}{98}\\ & ⟺\sin (\theta +30°)=\frac{91}{98}\\ & ⟺\tan (\theta +30°)=\frac{13\sqrt{3}}{9}\\ & ⟺\tan (\theta )=\frac{5\sqrt{3}}{11}\end{array}$$

Problem 2

Suppose $A$, $B$ and $C$ are points in the plane with $|AB|=40$ and $|AC|=42$, and let $x$ be the length of the line segment from $A$ to the midpoint of $\overline{BC}$. Define a function $f$ by letting $f(x)$ be the area of $△ABC$. Then the domain of $f$ is an open interval $(p,q)$, and the maximum value $r$ of $f(x)$ occurs at $x=s$. What is $p+q+r+s$?

Solution

Applying the Triangle Inequality yields that $A$, $B$ and $C$ forms a triangle iff

$$||AB|-|AC||<|BC|<|AB|+|AC|⟺2<|BC|<82$$

Applying Apollonius’s Theorem yields

$$\begin{array}{rl}x& =\frac{1}{2}\sqrt{2|AB{|}^2+2|AC{|}^2-|BC{|}^2}\\ & =\frac{1}{2}\sqrt{6728-|BC{|}^2}\end{array}$$

Therefore, $A$, $B$ and $C$ forms a triangle iff

$$1<x<41$$

Therefore, $p=1,q=41$.

$$\begin{array}{rl}f(x)& =[△ABC]\\ & =\frac{1}{2}|AB||AC|\sin (\angle BAC)\\ & =840\sin (\angle BAC)\end{array}$$

Applying the Pythagorean Theorem yields

$$\begin{array}{rl}\angle BAC=90°& ⟺|AB{|}^2+|AC{|}^2=|BC{|}^2\\ & ⟺|BC|=58\\ & ⟺x=29\end{array}$$

Therefore, it is easy to prove that $r=840,s=29$. Therefore, $p+q+r+s=911$.

Problem 3

The measures of the smallest angles of three different right triangles sum to $90°$. All three triangles have side lengths that are primitive Pythagorean triples. Two of them are $3-4-5$ and $5-12-13$. What is the perimeter of the third triangle?

Solution

Let the smallest angles of these triangles be $\alpha$, $\beta$ and $\gamma$, respectively. Then

$$\begin{array}{rl}\tan (\gamma )& =\tan (90°-\alpha -\beta )\\ & =\cot (\alpha +\beta )\\ & =\frac{\cot (\alpha )\cot (\beta )-1}{\cot (\alpha )+\cot (\beta )}\\ & =\frac{33}{56}\end{array}$$

Therefore, it is easy to prove that the third triangle is a $33-56-65$ triangle. Therefore, the perimeter of the third triangle is $33+56+65=154$.

Problem 4

Let $△ABC$ be a triangle with integer side lengths and the property that $\angle B=2\angle A$. What is the least possible perimeter of such a triangle?

Solution

Applying the Law of Sines yields

$$\frac{|AC|}{|BC|}=\frac{\sin (\angle B)}{\sin (\angle A)}$$

Therefore,

$$\begin{array}{rl}\angle B=2\angle A& ⟹\sin (\angle B)=\sin (2\angle A)\\ & ⟺\frac{|AC|}{|BC|}=\frac{\sin (2\angle A)}{\sin (\angle A)}\\ & ⟺\frac{|AC|}{|BC|}=2\cos (\angle A)\end{array}$$

Applying the Law of Cosines yields

$$\cos (\angle A)=\frac{|AB{|}^2+|AC{|}^2-|BC{|}^2}{2|AB||AC|}$$

Therefore,

$$\begin{array}{rl}\angle B=2\angle A& ⟹\frac{|AC|}{|BC|}=\frac{|AB{|}^2+|AC{|}^2-|BC{|}^2}{|AB||AC|}\\ & ⟺|AB|=|BC|\vee |AC{|}^2=|BC|(|AB|+|BC|)\end{array}$$

Therefore, it is easy to prove that if $|AC|<7$, the only triangle with integer side lengths and the property that $\angle B=2\angle A$ is the triangle such that $|AB|=5\wedge |AC|=6\wedge |BC|=4$. The perimeter of this triangle is $5+6+4=15$.

Applying the Triangle Inequality yields

$$|AB|+|BC|>|AC|$$

Therefore, if $|AC|\ge 7$,

$$\begin{array}{rl}|AB|+|BC|>|AC|& ⟺|AB|+|AC|+|BC|>2|AC|\\ & ⟹|AB|+|AC|+|BC|\ge 15\end{array}$$

Therefore, the least perimeter is $15$.

Problem 5

A right pyramid has regular octagon $ABCDEFGH$ with side length $1$ as its base and apex $V$. Segments $\overline{AV}$ and $\overline{DV}$ are perpendicular. What is the square of the height of the pyramid?

Solution

Let $O$ be the center of the octagon, $X$ be a point on $\overline{BC}$ such that $\overline{OX}\perp \overline{BC}$, $Y$ be a point on $DE$ such that $\overline{OY}\perp \overline{DE}$. Set up a coordinate system by taking $O$ as the origin, $\overrightarrow{OX}$ as the $x$-axis, $\overrightarrow{OY}$ as the $y$-axis, and $\overrightarrow{OV}$ as the $z$-axis. Then it is easy to prove that

$$\overrightarrow{OA}=\left(\frac{1}{2},-\frac{1+\sqrt{2}}{2},0\right),\overrightarrow{OD}=\left(\frac{1}{2},-\frac{1+\sqrt{2}}{2},0\right),\overrightarrow{OV}=(0,0,|OV|)$$

Therefore,

$$\begin{array}{rl}\overrightarrow{AV}& =\overrightarrow{OV}-\overrightarrow{OA}\\ & =\left(-\frac{1}{2},\frac{1+\sqrt{2}}{2},|OV|\right)\end{array}$$ $$\begin{array}{rl}\overrightarrow{DV}& =\overrightarrow{OV}-\overrightarrow{OD}\\ & =\left(-\frac{1}{2},-\frac{1+\sqrt{2}}{2},|OV|\right)\end{array}$$

Therefore,

$$\begin{array}{rl}AV\perp DV& ⟺\overrightarrow{AV}\cdot \overrightarrow{DV}=0\\ & ⟺-\frac{1+\sqrt{2}}{2}+|OV{|}^2=0\\ & ⟺|OV{|}^2=\frac{1+\sqrt{2}}{2}\end{array}$$

Therefore, the square of the height is $\frac{1+\sqrt{2}}{2}$.

Problem 6

What is the number of ordered triples $⟨a,b,c⟩$ of positive integers, with $a\le b\le c\le 9$, such that there exists a (non-degenerate) triangle $△ABC$ with an integer inradius for which $a$, $b$ and $c$ are the lengths of the altitudes from $A$ to $\overline{BC}$, $B$ to $\overline{AC}$, and $C$ to $\overline{AB}$, respectively?

Solution

Let $O$ be the incenter of $△ABC$, $r$ be the length of the inradius of $△ABC$. Then

$$\begin{array}{rl}[△ABC]& =[△AOB]+[△AOC]+[△BOC]\\ & =\frac{1}{2}(|AB|+|AC|+|BC|)r\end{array}$$

Since $[△ABC]=\frac{1}{2}|AB|c$, it follows that

$$\frac{r}{c}=\frac{|AB|}{|AB|+|AC|+|BC|}$$

Since $[△ABC]=\frac{1}{2}|AC|b$, it follows that

$$\frac{r}{b}=\frac{|AC|}{|AB|+|AC|+|BC|}$$

Since $[△ABC]=\frac{1}{2}|BC|a$, it follows that

$$\frac{r}{a}=\frac{|BC|}{|AB|+|AC|+|BC|}$$

Therefore,

$$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{r}$$

Therefore,

$$r\in \mathbb{Z}⟺\frac{1}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\in \mathbb{Z}$$

Therefore, it is easy to prove that all ordered triples are $⟨3,3,3⟩$, $⟨6,6,6⟩$, and $⟨9,9,9⟩$. Therefore, the number of ordered triples is $3$.

Problem 7

Cyclic quadrilateral $ABCD$ has lengths $|BC|=|CD|=3$ and $|AD|=5$ with $\angle ADC=120°$. What is the length of the shorter diagonal of $ABCD$?

Solution

Applying the Law of Cosines yields

$$|AC{|}^2=|AD{|}^2+|CD{|}^2-2|AD||CD|\cos (\angle ADC)$$ $$|AC{|}^2=|AD{|}^2+|CD{|}^2-2|AD||CD|\cos (\angle ADC)⟺|AC|=7$$

Applying the Law of Cosines yields

$$|AC{|}^2=|AB{|}^2+|BC{|}^2-2|AB||BC|\cos (\angle ABC)$$

Since

$$\begin{array}{rl}\angle ABC& =180°-\angle ADC\\ & =60°\end{array}$$

it follows that

$$|AC{|}^2=|AB{|}^2+|BC{|}^2-2|AB||BC|\cos (\angle ABC)⟺|AB|=8$$

Applying Ptolemy’s Theorem yields

$$|AC||BD|=|AB||CD|+|AD||BC|$$ $$|AC||BD|=|AB||CD|+|AD||BC|⟺|BD|=\frac{39}{7}$$

Therefore, the length of the shorter diagonal is $\min \{|AC|,|BD|\}=\frac{39}{7}$.

Problem 8

On top of a rectangular card with sides of length $1$ and $2+\sqrt{3}$, an identical card is placed so that two of their diagonals line up, as shown ($\overline{AC}$, in this case). Continue the process, adding a third card to the second, and so on, lining up successive diagonals after rotating clockwise. In total, how many cards must be used until a vertex of a new card lands exactly on the vertex $B$ in the figure?

Solution

Applying the Pythagorean Theorem yields

$$\begin{array}{rl}|AC|& =\sqrt{|AB{|}^2+|BC{|}^2}\\ & =2\sqrt{2+\sqrt{3}}\end{array}$$

Let $D$ be the midpoint of $\overline{AC}$, then

$$\begin{array}{rl}|AD|& =\frac{1}{2}|AC|\\ & =\sqrt{2+\sqrt{3}}\end{array}$$ $$\begin{array}{rl}|BD|& =|AD|\\ & =\sqrt{2+\sqrt{3}}\end{array}$$

Applying the Law of Cosines yields

$$|AB{|}^2=|AD{|}^2+|BD{|}^2-2|AD||BD|\cos (\angle ADB)$$ $$\begin{array}{rl}|AB{|}^2=|AD{|}^2+|BD{|}^2-2|AD||BD|\cos (\angle ADB)& ⟺\cos (\angle ADB)=\frac{\sqrt{3}}{2}\\ & ⟺\angle ADB=30°\end{array}$$

Therefore, it is easy to prove that $6$ cards must be used.

Problem 9

Triangle $△ABC$ has side lengths in arithmetic progression, and the smallest side has length $6$. If the triangle has an angle of $120°$, what is the area of $△ABC$?

Solution

Wlog, assume $|AB|\le |AC|\le |BC|$, then it is easy to prove that $|AB|=6$ and $\angle A=120°$.

Applying the Law of Cosines yields

$$|BC{|}^2=|AB{|}^2+|AC{|}^2-2|AB||AC|\cos (\angle A)$$

Let $d$ be common difference of the arithmetic progression, then

$$|BC{|}^2=|AB{|}^2+|AC{|}^2-2|AB||AC|\cos (\angle A)⟺d=4$$

Therefore, $|AC|=10$.

Therefore,

$$\begin{array}{rl}[△ABC]& =\frac{1}{2}\sin (\angle A)|AB||AC|\\ & =15\sqrt{3}\end{array}$$

Problem 10

A regular pentagon with area $1+\sqrt{5}$ is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?

Solution

Let $ABCDE$ be the pentagon, $O$ be the center of $ABCDE$, $M$ be the midpoint of $\overline{OA}$, $N$ be a point on $\overline{AB}$ such that $\overline{ON}\perp \overline{AB}$, $x$ be area of the new pentagon. Then it is easy to prove that

$$\begin{array}{rl}\frac{[ABCDE]}{x}& ={\left(\frac{|ON|}{|OM|}\right)}^2\\ & ={\left(\frac{2|ON|}{|OA|}\right)}^2\\ & =(2\sin (\angle AON){)}^2\\ & =4\sin (54°{)}^2\end{array}$$

Since

$$\begin{array}{rl}\cos (54°)=\sin (36°)& ⟺\cos (18°{)}^3-3\sin (18°{)}^2\cos (18°)=2\sin (18°)\cos (18°)\\ & ⟺4\sin (18°{)}^2+2\sin (18°)-1=0\\ & ⟺\sin (18°)=\frac{-1+\sqrt{5}}{4}\end{array}$$

it follows that

$$\begin{array}{rl}\sin (54°)& =\cos (36°)\\ & =1-2\sin (18°{)}^2\\ & =\frac{1+\sqrt{5}}{4}\end{array}$$

Therefore,

$$\begin{array}{rl}x& =\frac{[ABCDE]}{4\sin (54°{)}^2}\\ & =-1+\sqrt{5}\end{array}$$

Problem 11

Let $△PQR$ be a triangle with $\angle P=75°$ and $\angle Q=60°$. A regular hexagon $ABCDEF$ with side length $1$ is drawn inside $△PQR$ so that side $\overline{AB}$ lies on $\overline{PQ}$, side $\overline{CD}$ lies on $\overline{QR}$, and one of the remaining vertices lies on $\overline{PR}$. There are positive integers $a$, $b$, $c$, and $d$ such that the area of $△PQR$ can be expressed in the form $\frac{a+b\sqrt{c}}{d}$, where $a$ and $d$ are relatively prime, and $c$ is not divisible by the square of any prime. Find $a+b+c+d$.

Solution

Applying the Law of Sines yields

$$\begin{array}{rl}\frac{|PA|}{|PF|}& =\frac{\sin (\angle PFA)}{\sin (\angle APF)}\\ & =\frac{\sin (45°)}{\sin (75°)}\end{array}$$

Since

$$\begin{array}{rl}\sin (75°)& =\cos (15°)\\ & =\sqrt{\frac{1+\cos (30°)}{2}}\\ & =\frac{\sqrt{2}+\sqrt{6}}{4}\end{array}$$

it follows that

$$|PA|=-1+\sqrt{3}$$

Therefore,

$$\begin{array}{rl}|PQ|& =|PA|+|AB|+|BQ|\\ & =1+\sqrt{3}\end{array}$$

Since

$$\angle PAF=\angle Q⟺△PAF\sim △PQR$$

it follows that

$$\begin{array}{rl}\frac{[△PQR]}{[△PAF]}& ={\left(\frac{|PQ|}{|PA|}\right)}^2\\ & =7+4\sqrt{3}\end{array}$$

Since

$$\begin{array}{rl}[△PAF]& =\frac{1}{2}\sin (\angle PAF)|PA||AF|\\ & =\frac{3-\sqrt{3}}{4}\end{array}$$

it follows that

$$[△PQR]=\frac{9+5\sqrt{3}}{4}$$

Therefore, $a+b+c+d=21$.

Problem 12

In the figure below, semicircles with centers at $A$ and $B$ and with radii $2$ and $1$, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter $\overline{JK}$. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at $P$ is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at $P$?

Solution

Let $O$ be the center of the largest semicircle, $r$ be the length of the radius of $\odot P$, then it is easy to prove that $|AB|=3,|OA|=1,|OB|=2,|AP|=2+r,|BP|=1+r,|OP|=3-r$.

Applying Steward’s Theorem yields

$$|AP{|}^2|OB|+|BP{|}^2|OA|=|OP{|}^2|AB|+|OA||OB||AB|$$ $$|AP{|}^2|OB|+|BP{|}^2|OA|=(|OP{|}^2+|OA||OB|)|AB|⟺r=\frac{6}{7}$$

Problem 13

Point $B$ is on $\overline{AC}$ with $|AB|=9$ and $|BC|=21$. Point $D$ is not on $\overline{AC}$ so that $|AD|=|CD|$, and $|AD|$ and $|BD|$ are integers. Let $s$ be the sum of all possible perimeters of $△ACD$. Find $s$.

Solution

Let $E$ be the midpoint of $\overline{AC}$, then applying the Pythagorean Theorem yields

$$|AD{|}^2-|AE{|}^2=|DE{|}^2,|BD{|}^2-|BE{|}^2=|DE{|}^2$$

Therefore,

$$(|AD|-|BD|)(|AD|+|BD|)=189$$

Therefore, it is easy to prove that

$$|AD|\in \mathbb{Z}\wedge |BD|\in \mathbb{Z}⟺|AD|=95\vee |AD|=33\vee |AD|=17$$

Therefore, $s=380$.

Problem 14

In $△ABC$, $|AB|=13$, $|AC|=14$, and $|BC|=15$. Point $D$ is on $\overline{BC}$ with $|CD|=6$. Point $E$ is on $\overline{BC}$ such that $\angle BAE=\angle CAD$. Given that $|BE|=\frac{p}{q}$ where $p$ and $q$ are relatively prime positive integers, find $q$.

Solution

$$\begin{array}{rl}\frac{|BE|}{|CE|}& =\frac{[△ABE]}{[△ACE]}\\ & =\frac{\frac{1}{2}\sin (\angle BAE)|AB||AE|}{\frac{1}{2}\sin (\angle CAE)|AC||AE|}\\ & =\frac{13\sin (\angle BAE)}{14\sin (\angle CAE)}\end{array}$$

Since

$$\begin{array}{rl}\frac{|BD|}{|CD|}& =\frac{[△ABD]}{[△ACD]}\\ & =\frac{\frac{1}{2}\sin (\angle BAD)|AB||AD|}{\frac{1}{2}\sin (\angle CAD)|AC||AD|}\\ & =\frac{13\sin (\angle BAD)}{14\sin (\angle CAD)}\end{array}$$

it follows that

$$\begin{array}{rl}\frac{\sin (\angle BAE)}{\sin (\angle CAE)}& =\frac{\sin (\angle CAD)}{\sin (\angle BAD)}\\ & =\frac{13|CD|}{14|BD|}\\ & =\frac{13}{21}\end{array}$$

Therefore,

$$\frac{|BE|}{|CE|}=\frac{169}{294}$$ $$\begin{array}{rl}\frac{|BE|}{|CE|}=\frac{169}{294}& ⟺|BE|=\frac{169}{463}|BC|\\ & ⟺|BE|=\frac{2535}{463}\end{array}$$

Therefore, $q=463$.

Problem 15

A paper equilateral triangle $△ABC$ has side length $12$. The paper triangle is folded so that vertex $A$ touches a point on side $\overline{BC}$ a distance $9$ from point $B$. The length of the line segment along which the triangle is folded can be written as $\frac{m\sqrt{p}}{n}$, where $m$, $n$, and $p$ are positive integers, $m$ and $n$ are relatively prime, and $p$ is not divisible by the square of any prime. Find $m+n+p$.

Solution

Let $D$ be the point on $\overline{BC}$, $M$ be the point on $\overline{AB}$. Then applying the Law of Cosines yields

$$|MD{|}^2=|MB{|}^2+|BD{|}^2+2|MB||BD|\cos (\angle B)$$ $$|MD{|}^2=|MB{|}^2+|BD{|}^2+2|MB||BD|\cos (\angle B)⟺|AM|=\frac{39}{5}$$

Let $N$ be the point on $\overline{AC}$, then applying the Law of Cosines yields

$$|ND{|}^2=|NC{|}^2+|CD{|}^2+2|NC||CD|\cos (\angle C)$$ $$|ND{|}^2=|NC{|}^2+|CD{|}^2+2|NC||CD|\cos (\angle C)⟺|AN|=\frac{39}{7}$$

Applying the Law of Cosines yields

$$\begin{array}{rl}|MN|& =\sqrt{|AM{|}^2+|AN{|}^2+2|AM||AN|\cos (\angle A)}\\ & =\frac{39\sqrt{39}}{35}\end{array}$$

Therefore, $m+n+p=113$.

Problem 16

Let $△ABC$ be an acute triangle with circumcenter $O$ and centroid $G$. Let $X$ be the intersection of the line tangent to the circumcircle of $△ABC$ at $A$ and the line perpendicular to $\overline{GO}$ at $G$. Let $Y$ be the intersection of lines $\overleftrightarrow{XG}$ and $\overleftrightarrow{BC}$. Given that the measures of $\angle ABC$, $\angle ACB$, and $\angle XOY$ are in the ratio $13:2:17$, the degree measure of $\angle BAC$ can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Solution

Since $\angle XGO=\angle XAO$, it follows that $XOGA$ is cyclic. Since $XOGA$ is cyclic, it follows that $\angle GAO=\angle GXO$.

Let $M$ be the midpoint of $\overline{BC}$, then since $\angle YMO+\angle YGO=180°$, it follows that $MOGY$ is cyclic. Since $MOGY$ is cyclic, it follows that $\angle GMO=\angle GYO$.

$$\begin{array}{rl}\angle GAO=\angle GXO\wedge \angle GMO=\angle GYO& ⟺△AOM\sim △XOY\\ & ⟹\angle AOM=\angle XOY\end{array}$$

Therefore,

$$\begin{array}{rl}\angle BAC& =\frac{1}{2}\angle BOC\\ & =\angle BOM\\ & =\angle AOM-\angle AOB\\ & =\angle XOY-2\angle ACB\end{array}$$

Therefore,

$$\begin{array}{rl}\angle ABC:\angle ACB:\angle XOY=13:2:17& ⟺\angle BAC:\angle ABC:\angle ACB=13:13:2\\ & ⟹\angle BAC=\frac{585}{7}°\end{array}$$

Therefore, $m+n=592$.

Problem 17

In $△ABC$ we have $|AB|=7,|AC|=8,|BC|=9$. Point $D$ is on the circumscribed circle of the triangle so that $\overline{AD}$ bisects $\angle BAC$. What is the value of $\frac{|AD|}{|CD|}$?

Solution

$$\begin{array}{rl}\angle BAD=\angle CAD& ⟺\angle BCD=\angle CBD\\ & ⟺|BD|=|CD|\end{array}$$

Therefore, applying Ptolemy’s Theorem yields

$$|AB||CD|+|AC||BD|=|AD||BC|⟺\frac{|AD|}{|CD|}=\frac{5}{3}$$

Problem 18

Two externally tangent circles ${\omega }_1$ and ${\omega }_2$ have centers $O_1$ and $O_2$, respectively. A third circle $\Omega$ passing through $O_1$ and $O_2$ intersects ${\omega }_1$ at $B$ and $C$ and ${\omega }_2$ at $A$ and $D$, as shown. Suppose that $|AB|=2,|O_1{O}_2|=15,|CD|=16$, and $AB{O}_{1}CD{O}_2$ is a convex hexagon. Find the area of this hexagon.

Solution

Let $A^{\prime }$ and $B^{\prime }$ be the reflections of $A$ and $B$, respectively, about the perpendicular bisector of $\overline{O_1{O}_2}$. Then it is easy to prove that $A^{\prime }$ and $B^{\prime }$ are on $\Omega$ and $O_1{O}_{2}AB\cong O_2{O}_1{A}^{\prime }{B}^{\prime }$.

$$\begin{array}{rl}|O_1{A}^{\prime }|& =|O_{2}A|\\ & =|O_{2}D|\end{array}$$

Since

$$\begin{array}{rl}|O_1{A}^{\prime }|=|O_{2}D|& ⟺\widehat{O_1{A}^{\prime }}=\widehat{O_{2}D}\\ & ⟺\angle O_1{O}_2{A}^{\prime }=\angle O_2{O}_{1}D\\ & ⟺\overline{O_2{A}^{\prime }}\parallel \overline{O_{1}D}\end{array}$$

it follows that $O_1{A}^{\prime }{O}_{2}D$ is an isosceles trapezoid.

Therefore,

$$\begin{array}{rl}|A^{\prime }D|& =|O_1{O}_2|\\ & =15\end{array}$$ $$\begin{array}{rl}|O_2{B}^{\prime }|& =|O_{1}B|\\ & =|O_{1}C|\end{array}$$

Since

$$\begin{array}{rl}|O_2{B}^{\prime }|=|O_{1}C|& ⟺\widehat{O_2{B}^{\prime }}=\widehat{O_{1}C}\\ & ⟺\angle O_1{B}^{\prime }C=\angle O_{2}C{B}^{\prime }\\ & ⟺\overline{O_1{B}^{\prime }}\parallel \overline{O_{2}C}\end{array}$$

it follows that $O_1{B}^{\prime }{O}_{2}C$ is an isosceles trapezoid.

Therefore,

$$\begin{array}{rl}|B^{\prime }C|& =|O_1{O}_2|\\ & =15\end{array}$$ $$\widehat{O_1{A}^{\prime }}=\widehat{O_{2}D}⟺\angle O_{1}C{A}^{\prime }=\angle O_2{B}^{\prime }D$$ $$\widehat{O_{1}C}=\widehat{O_2{B}^{\prime }}⟺\angle O_1{A}^{\prime }C=\angle O_{2}D{B}^{\prime }$$

Since

$$\begin{array}{rl}\angle O_{1}C{A}^{\prime }=\angle O_2{B}^{\prime }D\wedge \angle O_1{A}^{\prime }C=\angle O_{2}D{B}^{\prime }\wedge |O_1{A}^{\prime }|=|O_{2}D|& ⟺△O_1{A}^{\prime }C\cong △O_{2}D{B}^{\prime }\\ & ⟹|A^{\prime }C|=|B^{\prime }D|\\ & ⟺\widehat{A^{\prime }C}=\widehat{B^{\prime }D}\\ & ⟺\angle A^{\prime }{B}^{\prime }C=\angle B^{\prime }CD\\ & ⟺\overline{A^{\prime }{B}^{\prime }}\parallel \overline{CD}\end{array}$$

it follows that $A^{\prime }{B}^{\prime }DC$ is an isosceles trapezoid.

Therefore, applying Ptolemy’s Theorem yields

$$|A^{\prime }{B}^{\prime }||CD|+|A^{\prime }C||B^{\prime }D|=|A^{\prime }D||B^{\prime }C|$$ $$|A^{\prime }{B}^{\prime }||CD|+|A^{\prime }C||B^{\prime }D|=|A^{\prime }D||B^{\prime }C|⟺|A^{\prime }C|=\sqrt{193}$$

Therefore, applying the Law of Cosines yields

$$\begin{array}{rl}\cos (\angle A^{\prime }{B}^{\prime }C)& =\frac{|A^{\prime }{B}^{\prime }{|}^2+|B^{\prime }C{|}^2-|A^{\prime }C{|}^2}{2|A^{\prime }{B}^{\prime }||B^{\prime }C|}\\ & =\frac{3}{5}\end{array}$$ $$\cos (\angle A^{\prime }{B}^{\prime }C)=\frac{3}{5}⟺\sin (\angle A^{\prime }{B}^{\prime }C)=\frac{4}{5}$$

Let $E$ be perpendicular foot from $C$ to $\overleftrightarrow{A^{\prime }{B}^{\prime }}$, then it follows that

$$\begin{array}{rl}|CE|& =|B^{\prime }C|\sin (\angle A^{\prime }{B}^{\prime }C)\\ & =12\end{array}$$

Therefore,

$$\begin{array}{rl}[A^{\prime }{B}^{\prime }DC]& =\frac{1}{2}(|A^{\prime }{B}^{\prime }|+|CD|)|CE|\\ & =108\end{array}$$

Let $r_1$ and $r_2$ be the radius of ${\omega }_1$ and ${\omega }_2$, respectively. Then it follows that

$$\begin{array}{rl}{r}_1+r_2& =|O_1{O}_2|\\ & =15\end{array}$$

Applying the Law of Cosines yields

$$|A^{\prime }C{|}^2=|O_1{A}^{\prime }{|}^2+|O_{1}C{|}^2-2|O_1{A}^{\prime }||O_{1}C|\cos (\angle A^{\prime }{O}_{1}C)$$

Since

$$\begin{array}{rl}\cos (\angle A^{\prime }{O}_{1}C)& =\cos (180°-\angle A^{\prime }{B}^{\prime }C)\\ & =-\cos (\angle A^{\prime }{B}^{\prime }C)\\ & =-\frac{3}{5}\end{array}$$

it follows that

$$r_1{r}_2=40$$

Since

$$\begin{array}{rl}\sin (\angle A^{\prime }{O}_{1}C)& =\cos (180°-\angle A^{\prime }{B}^{\prime }C)\\ & =\sin (\angle A^{\prime }{B}^{\prime }C)\\ & =\frac{4}{5}\end{array}$$

it follows that

$$\begin{array}{rl}[△O_1{A}^{\prime }C]& =\frac{1}{2}\sin (\angle A^{\prime }{O}_{1}C)|O_1{A}^{\prime }||O_{1}C|\\ & =\frac{2}{5}{r}_1{r}_2\\ & =16\end{array}$$

Therefore,

$$\begin{array}{rl}[△O_{2}D{B}^{\prime }]& =[△O_1{A}^{\prime }C]\\ & =16\end{array}$$

Therefore,

$$\begin{array}{rl}[AB{O}_{1}CD{O}_2]& =[O_1{O}_{2}AB]+[O_1{O}_{2}CD]\\ & =[O_2{O}_1{A}^{\prime }{B}^{\prime }]+[O_1{O}_{2}CD]\\ & =[O_1{A}^{\prime }{B}^{\prime }{O}_{2}DC]\\ & =[A^{\prime }{B}^{\prime }DC]+[△O_1{A}^{\prime }C]+[△O_{2}D{B}^{\prime }]\\ & =140\end{array}$$

Problem 19

Quadrilateral $ABCD$ is inscribed in $\odot O$ and has side lengths $|AB|=3$, $|BC|=2$, $|CD|=6$, and $|AD|=8$. Let $X$ and $Y$ be points on $\overline{BD}$ such that $\frac{|DX|}{|BD|}=\frac{1}{4}$ and $\frac{|BY|}{|BD|}=\frac{11}{36}$. Let $E$ be the intersection of line $\overleftrightarrow{AX}$ and the line through $Y$ parallel to $\overline{AD}$. Let $F$ be the intersection of the line $\overleftrightarrow{CX}$ and the line through $E$ parallel to $\overleftrightarrow{AC}$. Let $G$ be the point on $\odot O$ other than $C$ that lies on line $\overleftrightarrow{CX}$. What is $|FX||GX|$?

Solution

$$\begin{array}{rl}\overline{EY}\parallel \overline{AG}& ⟺△ADX\sim △EYX\\ & ⟹\frac{|AX|}{|EX|}=\frac{DX}{XY}\\ & ⟺\frac{|AX|}{|EX|}=\frac{9}{16}\end{array}$$

Therefore,

$$\begin{array}{rl}\overline{AC}\parallel \overline{EF}& ⟺△ACX\sim △EFX\\ & ⟹\frac{|CX|}{|FX|}=\frac{|AX|}{|EX|}\\ & ⟺\frac{|CX|}{|FX|}=\frac{9}{16}\end{array}$$

Applying the Law of Cosines yields

$$\begin{array}{rl}|BD{|}^2& =|AB{|}^2+|AD{|}^2-2|AB||AD|\cos (\angle BAD)\\ & =73-48\cos (\angle BAD)\end{array}$$

Applying the Law of Cosines yields

$$\begin{array}{rl}|BD{|}^2& =|BC{|}^2+|CD{|}^2-2|BC||CD|\cos (\angle BCD)\\ & =40-24\cos (\angle BCD)\\ & =40+24\cos (\angle BAD)\end{array}$$

Therefore,

$$|BD|=\sqrt{51}$$

Therefore,

$$\begin{array}{rl}|DX|& =\frac{1}{4}|BD|\\ & =\frac{\sqrt{51}}{4}\end{array}$$

Therefore,

$$\begin{array}{rl}|BX|& =|BD|-|DX|\\ & =\frac{3\sqrt{51}}{4}\end{array}$$

Applying the Power of a Point Theorem yields

$$\begin{array}{rl}|CX||GX|& =|BX||DX|\\ & =\frac{153}{16}\end{array}$$

Therefore,

$$\begin{array}{rl}|FX||GX|& =\frac{|FX|}{|CX|}|CX||GX|\\ & =17\end{array}$$

Problem 20

In $△ABC$, $\angle A=40°$, $|AB|=10$, and $|AC|=6$. Points $D$ and $E$ lie on $\overline{AB}$ and $\overline{AC}$ respectively. What is the minimum possible value of $|BE|+|DE|+|CD|$?

Solution

Let $B^{\prime }$ be the reflection of $B$ about $\overleftrightarrow{AC}$, then $|B^{\prime }E|=|BE|$. Let $C^{\prime }$ be the reflection of $C$ about $\overleftrightarrow{AB}$, then $|C^{\prime }D|=|CD|$.

Since applying the Law of Cosines yields

$$\begin{array}{rl}|B^{\prime }{C}^{\prime }|& =\sqrt{|A{B}^{\prime }{|}^2+|A{C}^{\prime }{|}^2-2|A{B}^{\prime }||A{C}^{\prime }|\cos (\angle B^{\prime }A{C}^{\prime })}\\ & =14\end{array}$$

it follows that

$$\begin{array}{rl}\min (|BE|+|DE|+|CD|)& =\min (|B^{\prime }E|+|DE|+|C^{\prime }D|)\\ & =|B^{\prime }{C}^{\prime }|\\ & =14\end{array}$$

Problem 21

Cube $ABCDEFGH$, labeled as shown below, has edge length of $1$ and is cut by a plane passing through vertex $D$ and the midpoints $M$ and $N$ of $\overline{AB}$ and $\overline{CG}$ respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.

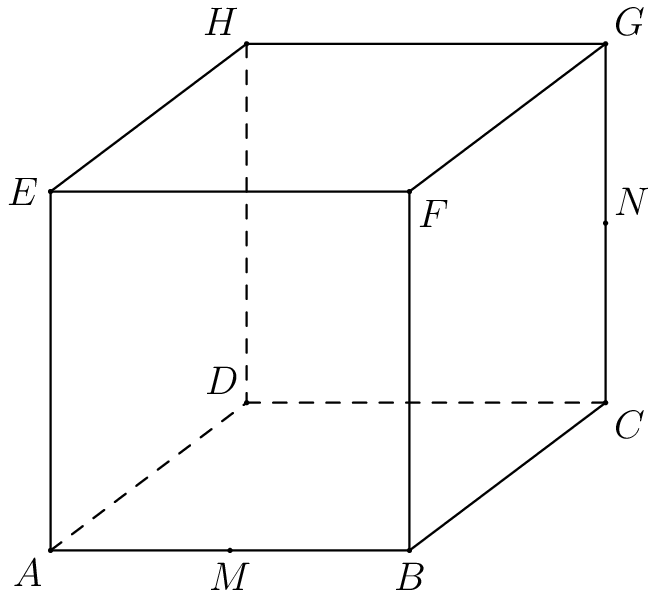
Solution

Set up a coordinate system by taking $D$ as the origin, $\overrightarrow{DA}$ as the $x$-axis, $\overrightarrow{DC}$ as the $y$-axis, and $\overrightarrow{DH}$ as the $z$-axis, then $M=(1,\frac{1}{2},0),N=(0,1,\frac{1}{2})$. Therefore, the plane is $z=-\frac{1}{4}x+\frac{1}{2}y$.

Therefore, the volume of one of the solids is

$${\int }_0^1{\int }_{\frac{1}{2}x}^1\left(-\frac{1}{4}x+\frac{1}{2}y\right)\mathrm{d}y\mathrm{d}x=\frac{7}{48}$$

Therefore, the volume of the larger solid is $1-\frac{7}{48}=\frac{41}{48}$. Therefore, $p+q=89$.

Problem 22

Tetrahedron $ABCD$ has $|AB|=5$, $|AC|=3$, $|BC|=4$, $|AD|=3$, $|BD|=4$, and $|CD|=\frac{12\sqrt{2}}{5}$. What is the volume of the tetrahedron?

Solution

Applying the Pythagorean Theorem yields

$$|AB{|}^2=|AC{|}^2+|BC{|}^2⟺\angle ACB=90°$$

Let $E$ be the perpendicular foot from $C$ to $\overline{AB}$, then

$$\begin{array}{rl}|CE|& =\frac{|AC||BC|}{|AB|}\\ & =\frac{12}{5}\end{array}$$

Similarly, it follows that $|DE|=\frac{12}{5}$.

Applying the Pythagorean Theorem yields

$$|CD{|}^2=|CE{|}^2+|DE{|}^2⟺\angle CED=90°$$

Therefore,

$$\begin{array}{rl}[ABCD]& =\frac{1}{3}[△ABC]|DE|\\ & =\frac{1}{6}|AC||BC||DE|\\ & =\frac{24}{5}\end{array}$$

Problem 23

Inside a right circular cone with base radius $5$ and height $12$ are three congruent spheres with radius $r$. Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. What is $r$?

Solution

Let $O$ be the center of one of the spheres, $D$ be the point where that sphere is tangent to the base, $E$ be the point where that sphere is tangent to the side, $B$ be the center of the base, $A$ be the point such that $\overline{AB}$ is a radius of the base containing $D$, $C$ be the vertex of the cone. Then applying the Pythagorean Theorem yields

$$\begin{array}{rl}|AC|& =\sqrt{|AB{|}^2+|BC{|}^2}\\ & =13\end{array}$$ $$\overline{OD}\perp \overline{AB}\wedge \overline{OE}\perp \overline{AC}\wedge |OD|=|OE|⟹\angle OAB=\angle OAC$$

Therefore, let $F$ be the intersection of $\overleftrightarrow{OA}$ and $\overline{BC}$, then applying the Angle Bisector Theorem yields

$$\frac{|BF|}{|CF|}=\frac{|AB|}{|AC|}$$ $$\frac{|BF|}{|CF|}=\frac{|AB|}{|AC|}⟺|BF|=\frac{10}{3}$$

Therefore,

$$\begin{array}{rl}\overline{OD}\parallel \overline{BF}& ⟺△OAD\sim △FAB\\ & ⟹\frac{|AD|}{|AB|}=\frac{|OD|}{|BF|}\\ & ⟺|AD|=\frac{3}{2}r\end{array}$$

Let $X,Y$ be the center of the other spheres, respectively, then it is easy to prove that $△OXY$ is an equilateral triangle with center $B$ and side length $2r$.

Therefore, it is easy to prove that $|BD|=\frac{2\sqrt{3}}{3}r$.

Therefore,

$$|AD|+|BD|=|AB|⟺r=\frac{90-40\sqrt{3}}{11}$$

Problem 24

Three numbers in the interval $[0,1]$ are chosen independently and at random. What is the probability that the chosen numbers are the side lengths of a triangle with positive area?

Solution

Let the numbers be $x$, $y$, and $z$, respectively, then applying the Triangle Inequality yields $x$, $y$, and $z$ form a triangle iff

$$y+z>x\wedge x+z>y\wedge x+y>z$$

Therefore, the probability that $x$, $y$, and $z$ form a triangle is

$$\mathrm{Pr}[y+z>x\wedge x+z>y\wedge x+y>z]$$

Applying the Law of Total Probability yields

$$\begin{array}{rl}\mathrm{Pr}[y+z>x\wedge x+z>y\wedge x+y>z]& =\mathrm{Pr}[y+z>x\mid x>y\wedge x>z]\\ & =\frac{\mathrm{Pr}[y+z>x\wedge x>y\wedge x>z]}{\mathrm{Pr}[x>y\wedge x>z]}\\ & =3{\int }_0^1{\int }_0^1{\int }_0^1[y+z>x\wedge x>y\wedge x>z]\mathrm{d}z\mathrm{d}y\mathrm{d}x\\ & =3{\int }_0^1{\int }_0^x{\int }_{x-y}^x\mathrm{d}z\mathrm{d}y\mathrm{d}x\\ & =\frac{1}{2}\end{array}$$

Problem 25

Real numbers $x$, $y$, and $z$ are chosen independently and at random from the interval $[0,n]$ for some positive integer $n$. The probability that no two of $x$, $y$, and $z$ are within $1$ unit of each other is greater than $\frac{1}{2}$. What is the smallest possible value of $n$?

Solution

Since it is easy to prove that the probability is $0$ when $n=1$, it follows that $n\ge 2$.

Assume $n\ge 2$.

Applying the Law of Total Probability yields

$$\begin{array}{rl}\mathrm{Pr}[|x-y|>1\wedge |x-z|>1\wedge |y-z|>1]& =\mathrm{Pr}[x-y>1\wedge y-z>1\mid x>y>z]\\ & =\frac{\mathrm{Pr}[x-y>1\wedge y-z>1]}{\mathrm{Pr}[x>y>z]}\\ & =\frac{6}{n^3}{\int }_0^n{\int }_0^n{\int }_0^n[x-y>1\wedge y-z>1]\mathrm{d}z\mathrm{d}y\mathrm{d}x\\ & =\frac{6}{n^3}{\int }_2^n{\int }_1^{x-1}{\int }_0^{y-1}\mathrm{d}z\mathrm{d}y\mathrm{d}x\\ & =\frac{(n-2{)}^3}{n^3}\end{array}$$

Since

$$\frac{(n-2{)}^3}{n^3}>\frac{1}{2}⟺n\ge 10$$

it follows that the smallest possible value of $n$ is $10$.

Problem 26

Equilateral $△ABC$ has side length $600$. Points $P$ and $Q$ lie outside the plane of $△ABC$ and are on opposite sides of the plane. Furthermore, $|PA|=|PB|=|PC|$, and $|QA|=|QB|=|QC|$, and the planes of $△PAB$ and $△QAB$ form a $120°$ diheral angle. There is a point $O$ whose distance from each of $A,B,C,P,Q$ is $d$. Find $d$.

Solution

Let $D$ be the center of $△ABC$, then it is easy to prove that $\overline{PQ}\perp △ABC$ and the perpendicular foot is $D$.

Since $|OA|=|OB|=|OC|$ and $|OP|=|OQ|$, it follows that $O$ is on $\overline{PQ}$.

Therefore, applying the Pythagorean Theorem yields

$$|OA{|}^2=|OD{|}^2+|AD{|}^2$$

Let $x=|PD|,y=|QD|$, then

$$\begin{array}{rl}|OA{|}^2=|OD{|}^2+|AD{|}^2& ⟺{\left(\frac{x+y}{2}\right)}^2={\left(\frac{x-y}{2}\right)}^2+(200\sqrt{3}{)}^2\\ & ⟺xy=120000\end{array}$$

Let $E$ be the perpendicular foot from $D$ to $\overline{AB}$, then

$$\begin{array}{rl}\angle PEQ=120°& ⟺\angle PED+\angle QED=120°\\ & ⟺\tan (\angle PED+\angle QED)=-\sqrt{3}\\ & ⟺\frac{\tan (\angle PED)+\tan (\angle QED)}{1-\tan (\angle PED)\tan (\angle QED)}=-\sqrt{3}\\ & ⟺\frac{\frac{x}{100\sqrt{3}}+\frac{y}{100\sqrt{3}}}{1-\frac{x}{100\sqrt{3}}\frac{y}{100\sqrt{3}}}=-\sqrt{3}\\ & ⟺x+y=\frac{xy}{100}-300\\ & ⟺x+y=900\end{array}$$

Therefore,

$$\begin{array}{rl}d& =|OP|\\ & =\frac{x+y}{2}\\ & =450\end{array}$$

Problem 27

A $4\times 4\times h$ rectangular box contains a sphere of radius $2$ and eight smaller spheres of radius $1$. The smaller spheres are each tangent to three sides of the box, and the larger sphere is tangent to each of the smaller spheres. What is $h$?

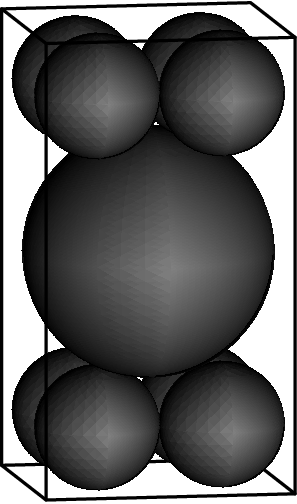
Solution

Let $A$ be the center of the larger sphere, $B,C,D,E$ be the centers of the smaller spheres below the larger sphere, respectively. Then it is easy to prove that $|BC|=|CD|=|DE|=|BE|=2$ and $|AB|=|AC|=|AD|=|AE|=3$.

Therefore, let $O$ be the center of $BCDE$, then it is easy to prove that $\overline{OA}\perp BCDE$.

Therefore, applying the Pythagorean Theorem yields

$$\begin{array}{rl}|OA|& =\sqrt{|AB{|}^2-|OB{|}^2}\\ & =\sqrt{7}\end{array}$$

Therefore, it is easy to prove that $h=2+2\sqrt{7}$.

Problem 28

A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?

Solution

Let $r$ be the radius of the top base of the truncated cone, $R$ be the radius of the bottom base of the truncated cone, $s$ be the radius of the sphere. Then applying the Pythagorean Theorem yields

$$(R+r{)}^2=(R-r{)}^2+(2s{)}^2$$ $$(R+r{)}^2=(R-r{)}^2+(2s{)}^2⟺s^2=Rr$$

Since the volume of the truncated cone is twice the volume of the sphere, it follows that

$$2\cdot \frac{4}{3}\pi s^3=\frac{1}{3}\pi (2s)(R^2+Rr+r^2)$$ $$\begin{array}{rl}2\cdot \frac{4}{3}\pi s^3=\frac{1}{3}\pi (2s)(R^2+Rr+r^2)& ⟺4s^2=R^2+Rr+r^2\\ & ⟺4Rr=R^2+Rr+r^2\\ & ⟺\frac{R}{r}=\frac{3+\sqrt{5}}{2}\end{array}$$

Problem 29

Suppose that $△ABC$ is an equilateral triangle of side length $s$, with property that there is a unique point $P$ inside the triangle such that $|AP|=1$, $|BP|=\sqrt{3}$, and $|CP|=2$. What is $s$?

Solution

Let $Q$ be the point obtained by rotating $P$ $60°$ counterclockwise about $A$. Then

$$\begin{array}{rl}\angle PAQ& =\angle CAP+\angle CAQ\\ & =\angle CAP+\angle BAP\\ & =\angle BAC\\ & =60°\end{array}$$ $$|AP|=|AQ|\wedge \angle PAQ=60°⟺|PQ|=1$$

Therefore, applying the Pythagorean Theorem yields

$$|CP{|}^2=|CQ{|}^2+|PQ{|}^2⟺\angle CQP=90°$$

Since

$$\begin{array}{rl}\angle CPQ& =\arccos \left(\frac{|PQ|}{|CP|}\right)\\ & =60°\end{array}$$

it follows that

$$\begin{array}{rl}\angle APC& =\angle APQ+\angle CPQ\\ & =120°\end{array}$$

Therefore, applying the Law of Cosines yields

$$\begin{array}{rl}s& =|AC|\\ & =\sqrt{|AP{|}^2+|CP{|}^2-2|AP||CP|\cos (\angle APC)}\\ & =\sqrt{7}\end{array}$$